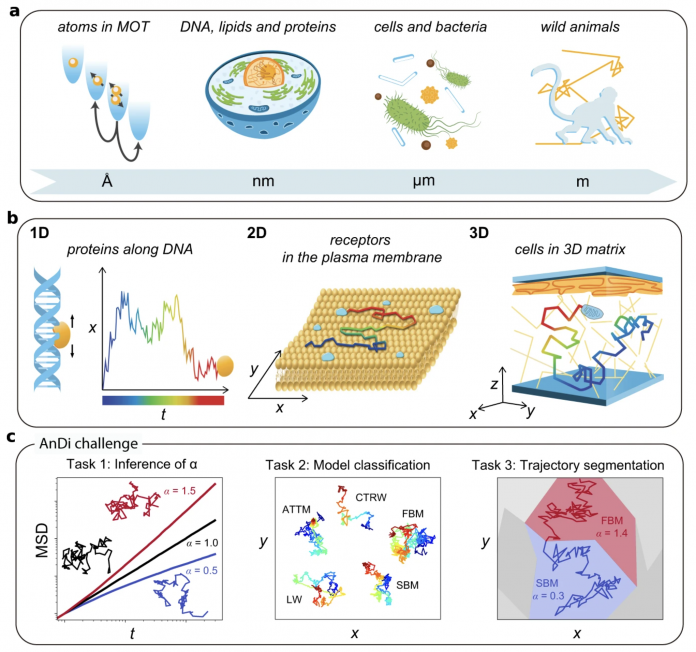
Deviations from Brownian motion leading to anomalous diffusion are found in transport dynamics from quantum physics to life sciences. The characterization of anomalous diffusion from the measurement of an individual trajectory is a challenging task, which traditionally relies on calculating the trajectory mean squared displacement. However, this approach breaks down for cases of practical interest, e.g., short or noisy trajectories, heterogeneous behavior, or non-ergodic processes. Recently, several new approaches have been proposed, mostly building on the ongoing machine-learning revolution. To perform an objective comparison of methods, we gathered the community and organized an open competition, the Anomalous Diffusion challenge (AnDi). Although no single method performed best across all scenarios, machine-learning-based approaches achieved superior performance for all tasks. The discussion of the challenge results provides practical advice for users and a benchmark for developers.
In this work, I have participated in this Challenge jointly with Òscar Garibo and Nicolàs Firbas. We developed the best model for the regression task in 1 dimension. Our models also show a great performance for the regression task in 2 and 3 dimensions, and for the classification tasks in all of them.
Our work has been published in Nature Communications. You can access to the content here https://www.nature.com/articles/s41467-021-26320-w