Anomalous diffusion (AD) describes transport phenomena where a particle’s mean-square displacement (MSD) does not scale linearly with time, deviating from classical diffusion. This behavior, often linked to non-equilibrium phenomena, sheds light on the underlying mechanisms in various systems, including biological and financial domains.
Integrating insights from anomalous diffusion into financial analysis could significantly improve our understanding of market behaviors, similar to their impacts on biological systems. In financial markets, accurately estimating asset volatility—whether historical or implied—is vital for investors.
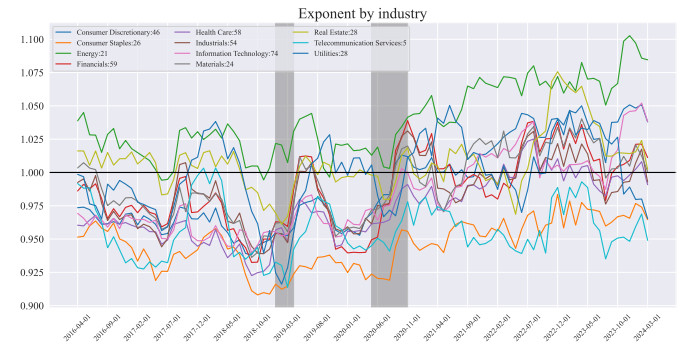
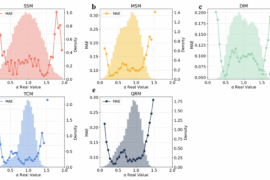
We introduce a novel methodology to estimate the volatility of stocks and similar assets, combining anomalous diffusion principles with machine learning. Our architecture combines convolutional and recurrent neural networks (bidirectional long short-term memory units). Our model computes the diffusion exponent of a financial time series to measure its volatility and it categorizes market movements into five diffusion models: annealed transit time motion (ATTM), continuous time random walk (CTRW), fractional Brownian motion (FBM), Lévy walk (LW), and scaled Brownian motion (SBM).
Our findings suggest that the diffusion exponent derived from anomalous diffusion processes provides insightful and novel perspectives on stock market volatility. By differentiating between subdiffusion, superdiffusion, and normal diffusion, our methodology offers a more nuanced understanding of market dynamics than traditional volatility metrics.
R.V. Arévalo, J.A. Conejero, Ò. Garibo-i-Orts, A. Peris. Stock volatility as an anomalous diffusion process. AIMS Math., 2024, 9(12): 34947-34965. doi: 10.3934/math.20241663
