Algorithms that use tensor decompositions are widely used due to how well they perfor with large amounts of data. Among them, we find the algorithms that search for the solution of a linear system in separated form, where the greedy rank-one update method stands out, to be the starting point of the famous proper generalized decomposition family. When the matrices of these systems have a particular structure, called a Laplacian-like matrix which is related to the aspect of the Laplacian operator, the convergence of the previous method is faster and more accurate.
The main goal of this paper is to provide a procedure that explicitly gives, for a given square matrix, its best approximation to the set of Laplacian-like matrices. Clearly, if the residue of this approximation is zero, we will be able to solve, by using the greedy rank-one update algorithm, the associated linear system at a lower computational cost. As a particular example, we prove that the discretization of a general partial differential equation of the second order without mixed derivatives can be written as a linear system with a Laplacian-type matrix. Finally, some numerical examples based on partial differential equations are given.
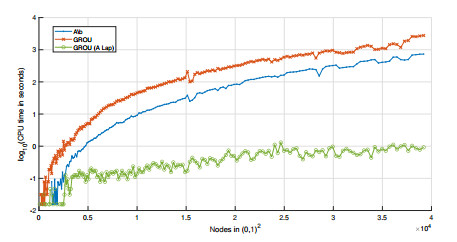
To sum up, in this work, we have studied the Laplacian decomposition algorithm, which, given any square matrix, calculates its best Laplacian approximation. For us, the greatest interest in this algorithm lies in the computational improvement of combining it with the GROU Algorithm 1 to solve linear systems through the discretization of a partial derivative equation. Said improvement can be seen in the different numerical examples shown, where we have compared this procedure with the standard resolution of Matlab by means of the instruction. This proposal is a new way of dealing with certain large-scale problems, where classical methods prove to be more inefficient.
You can have access (open) here:
J.A. Conejero, A., Falcó, M. Mora-Jiménez. A pre-processing procedure for the implementation of the greedy rank-one algorithm to solve high-dimensional linear systems. AIMS Math 8(11) 25633-25653 (2023). doi:10.3934/math.20231308